Information of spin space group $P\ce{^{1}{m}}\ce{^{1}{\text{-}3}}\ce{^{\text{-}1}{m}}\ce{^{\infty m}{1}}$ ( nSSG:200.221.1.1 )

General Positions

The continuously infinite group ^∞1 is omitted.

Coordinates	Seitz symbol
a, b, c | x, y, z	{ 1 ‖ 1 | 0 }
a, -b, -c | x, y, z	{ 1 ‖ 2100 | 0 }
-a, b, -c | x, y, z	{ 1 ‖ 2010 | 0 }
-a, -b, c | x, y, z	{ 1 ‖ 2001 | 0 }
c, a, b | x, y, z	{ 1 ‖ 3+111 | 0 }
b, c, a | x, y, z	{ 1 ‖ 3-111 | 0 }
-b, c, -a | x, y, z	{ 1 ‖ 3-1-1-1 | 0 }
-c, -a, b | x, y, z	{ 1 ‖ 3+1-1-1 | 0 }
-b, -c, a | x, y, z	{ 1 ‖ 3--11-1 | 0 }
c, -a, -b | x, y, z	{ 1 ‖ 3+-11-1 | 0 }
b, -c, -a | x, y, z	{ 1 ‖ 3--1-11 | 0 }
-c, a, -b | x, y, z	{ 1 ‖ 3+-1-11 | 0 }
-a, -b, -c | x, y, z	{ 1 ‖ -1 | 0 }
-a, b, c | x, y, z	{ 1 ‖ m100 | 0 }
a, -b, c | x, y, z	{ 1 ‖ m010 | 0 }
a, b, -c | x, y, z	{ 1 ‖ m001 | 0 }
-c, -a, -b | x, y, z	{ 1 ‖ -3+111 | 0 }
-b, -c, -a | x, y, z	{ 1 ‖ -3-111 | 0 }
b, -c, a | x, y, z	{ 1 ‖ -3-1-1-1 | 0 }
c, a, -b | x, y, z	{ 1 ‖ -3+1-1-1 | 0 }
b, c, -a | x, y, z	{ 1 ‖ -3--11-1 | 0 }
-c, a, b | x, y, z	{ 1 ‖ -3+-11-1 | 0 }
-b, c, a | x, y, z	{ 1 ‖ -3--1-11 | 0 }
c, -a, b | x, y, z	{ 1 ‖ -3+-1-11 | 0 }
a, -c, b | -x, -y, -z	{ -1 ‖ 4+100 | 0 }
a, c, -b | -x, -y, -z	{ -1 ‖ 4-100 | 0 }
c, b, -a | -x, -y, -z	{ -1 ‖ 4+010 | 0 }
-c, b, a | -x, -y, -z	{ -1 ‖ 4-010 | 0 }
-b, a, c | -x, -y, -z	{ -1 ‖ 4+001 | 0 }
b, -a, c | -x, -y, -z	{ -1 ‖ 4-001 | 0 }
b, a, -c | -x, -y, -z	{ -1 ‖ 2110 | 0 }
-b, -a, -c | -x, -y, -z	{ -1 ‖ 21-10 | 0 }
-a, c, b | -x, -y, -z	{ -1 ‖ 2011 | 0 }
-a, -c, -b | -x, -y, -z	{ -1 ‖ 201-1 | 0 }
c, -b, a | -x, -y, -z	{ -1 ‖ 2101 | 0 }
-c, -b, -a | -x, -y, -z	{ -1 ‖ 2-101 | 0 }
-a, c, -b | -x, -y, -z	{ -1 ‖ -4+100 | 0 }
-a, -c, b | -x, -y, -z	{ -1 ‖ -4-100 | 0 }
-c, -b, a | -x, -y, -z	{ -1 ‖ -4+010 | 0 }
c, -b, -a | -x, -y, -z	{ -1 ‖ -4-010 | 0 }
b, -a, -c | -x, -y, -z	{ -1 ‖ -4+001 | 0 }
-b, a, -c | -x, -y, -z	{ -1 ‖ -4-001 | 0 }
-b, -a, c | -x, -y, -z	{ -1 ‖ m110 | 0 }
b, a, c | -x, -y, -z	{ -1 ‖ m1-10 | 0 }
a, -c, -b | -x, -y, -z	{ -1 ‖ m011 | 0 }
a, c, b | -x, -y, -z	{ -1 ‖ m01-1 | 0 }
-c, b, -a | -x, -y, -z	{ -1 ‖ m101 | 0 }
c, b, a | -x, -y, -z	{ -1 ‖ m-101 | 0 }
a, b, c | -x, y, z	{ m ‖ 1 | 0 }
a, -b, -c | -x, y, z	{ m ‖ 2100 | 0 }
-a, b, -c | -x, y, z	{ m ‖ 2010 | 0 }
-a, -b, c | -x, y, z	{ m ‖ 2001 | 0 }
c, a, b | -x, y, z	{ m ‖ 3+111 | 0 }
b, c, a | -x, y, z	{ m ‖ 3-111 | 0 }
-b, c, -a | -x, y, z	{ m ‖ 3-1-1-1 | 0 }
-c, -a, b | -x, y, z	{ m ‖ 3+1-1-1 | 0 }
-b, -c, a | -x, y, z	{ m ‖ 3--11-1 | 0 }
c, -a, -b | -x, y, z	{ m ‖ 3+-11-1 | 0 }
b, -c, -a | -x, y, z	{ m ‖ 3--1-11 | 0 }
-c, a, -b | -x, y, z	{ m ‖ 3+-1-11 | 0 }
-a, -b, -c | -x, y, z	{ m ‖ -1 | 0 }
-a, b, c | -x, y, z	{ m ‖ m100 | 0 }
a, -b, c | -x, y, z	{ m ‖ m010 | 0 }
a, b, -c | -x, y, z	{ m ‖ m001 | 0 }
-c, -a, -b | -x, y, z	{ m ‖ -3+111 | 0 }
-b, -c, -a | -x, y, z	{ m ‖ -3-111 | 0 }
b, -c, a | -x, y, z	{ m ‖ -3-1-1-1 | 0 }
c, a, -b | -x, y, z	{ m ‖ -3+1-1-1 | 0 }
b, c, -a | -x, y, z	{ m ‖ -3--11-1 | 0 }
-c, a, b | -x, y, z	{ m ‖ -3+-11-1 | 0 }
-b, c, a | -x, y, z	{ m ‖ -3--1-11 | 0 }
c, -a, b | -x, y, z	{ m ‖ -3+-1-11 | 0 }
a, -c, b | x, -y, -z	{ 2 ‖ 4+100 | 0 }
a, c, -b | x, -y, -z	{ 2 ‖ 4-100 | 0 }
c, b, -a | x, -y, -z	{ 2 ‖ 4+010 | 0 }
-c, b, a | x, -y, -z	{ 2 ‖ 4-010 | 0 }
-b, a, c | x, -y, -z	{ 2 ‖ 4+001 | 0 }
b, -a, c | x, -y, -z	{ 2 ‖ 4-001 | 0 }
b, a, -c | x, -y, -z	{ 2 ‖ 2110 | 0 }
-b, -a, -c | x, -y, -z	{ 2 ‖ 21-10 | 0 }
-a, c, b | x, -y, -z	{ 2 ‖ 2011 | 0 }
-a, -c, -b | x, -y, -z	{ 2 ‖ 201-1 | 0 }
c, -b, a | x, -y, -z	{ 2 ‖ 2101 | 0 }
-c, -b, -a | x, -y, -z	{ 2 ‖ 2-101 | 0 }
-a, c, -b | x, -y, -z	{ 2 ‖ -4+100 | 0 }
-a, -c, b | x, -y, -z	{ 2 ‖ -4-100 | 0 }
-c, -b, a | x, -y, -z	{ 2 ‖ -4+010 | 0 }
c, -b, -a | x, -y, -z	{ 2 ‖ -4-010 | 0 }
b, -a, -c | x, -y, -z	{ 2 ‖ -4+001 | 0 }
-b, a, -c | x, -y, -z	{ 2 ‖ -4-001 | 0 }
-b, -a, c | x, -y, -z	{ 2 ‖ m110 | 0 }
b, a, c | x, -y, -z	{ 2 ‖ m1-10 | 0 }
a, -c, -b | x, -y, -z	{ 2 ‖ m011 | 0 }
a, c, b | x, -y, -z	{ 2 ‖ m01-1 | 0 }
-c, b, -a | x, -y, -z	{ 2 ‖ m101 | 0 }
c, b, a | x, -y, -z	{ 2 ‖ m-101 | 0 }

Wyckoff Positions

WP	Site symmetry	Representative
1a	$\ce{^{1}{m}}\ce{^{1}{-3}}\ce{^{-1}{m}}\ce{^{\infty m}{1}} $	(0,0,0 | 0,0,0)
1b	$\ce{^{1}{m}}\ce{^{1}{-3}}\ce{^{-1}{m}}\ce{^{\infty m}{1}} $	(1/2,1/2,1/2 | 0,0,0)
3c	$\ce{^{-1}{4}}/\ce{^{1}{m}}\ce{^{1}{m}}.\ce{^{-1}{m}}\ce{^{\infty m}{1}} $	(0,1/2,1/2 | 0,0,0)
3d	$\ce{^{-1}{4}}/\ce{^{1}{m}}\ce{^{1}{m}}.\ce{^{-1}{m}}\ce{^{\infty m}{1}} $	(1/2,0,0 | 0,0,0)
6e	$\ce{^{-1}{4}}\ce{^{1}{m}}.\ce{^{-1}{m}}\ce{^{\infty m}{1}} $	(a,0,0 | 0,0,0)
6f	$\ce{^{-1}{4}}\ce{^{1}{m}}.\ce{^{-1}{m}}\ce{^{\infty m}{1}} $	(a,1/2,1/2 | 0,0,0)
8g	$.\ce{^{1}{3}}\ce{^{-1}{m}}\ce{^{\infty m}{1}} $	(a,a,a | 0,0,0)
12h	$\ce{^{1}{2}}\ce{^{1}{m}}\ce{^{1}{m}}..\ce{^{\infty m}{1}} $	(a,1/2,0 | 0,0,z)
12i	$\ce{^{1}{m}}.\ce{^{-1}{2}}\ce{^{-1}{m}}\ce{^{\infty m}{1}} $	(0,b,b | 0,0,0)
12j	$\ce{^{1}{m}}.\ce{^{-1}{2}}\ce{^{-1}{m}}\ce{^{\infty m}{1}} $	(1/2,b,b | 0,0,0)
24k	$\ce{^{1}{m}}..\ce{^{\infty m}{1}} $	(0,b,c | 0,0,z)
24l	$\ce{^{1}{m}}..\ce{^{\infty m}{1}} $	(1/2,b,c | 0,0,z)
24m	$..\ce{^{-1}{m}}\ce{^{\infty m}{1}} $	(a,a,c | 0,0,0)
48n	$\ce{^{1}{1}}\ce{^{\infty m}{1}} $	(a,b,c | 0,0,z)

Spin Brillouin Zone & k-little co-groups

Wavevector-k	Little co-group
Γ:(0,0,0)	$\ce{^{1}{m}}\ce{^{1}{-3}}\ce{^{-1}{m}}\ce{^{\infty m}{1}} $
R:(1/2,1/2,1/2)	$\ce{^{1}{m}}\ce{^{1}{-3}}\ce{^{-1}{m}}\ce{^{\infty m}{1}} $
M:(1/2,1/2,0)	$\ce{^{-1}{4/}}\ce{^{1}{m}}\ce{^{1}{m}}\ce{^{-1}{m}}\ce{^{\infty m}{1}} $
X:(0,1/2,0)	$\ce{^{-1}{4/}}\ce{^{1}{m}}\ce{^{1}{m}}\ce{^{-1}{m}}\ce{^{\infty m}{1}} $
Δ:(0,v,0)	$\ce{^{2}{4/}}\ce{^{m}{m}}\ce{^{1}{m}}\ce{^{2}{m}}\ce{^{\infty}{1}} $
T:(1/2,1/2,w)	$\ce{^{2}{4/}}\ce{^{m}{m}}\ce{^{1}{m}}\ce{^{2}{m}}\ce{^{\infty}{1}} $
Λ:(u,u,u)	$\ce{^{m}{-3}}\ce{^{2}{m}}\ce{^{\infty}{1}} $
S:(u,1/2,u)	$\ce{^{-1}{m}}\ce{^{1}{m}}\ce{^{2}{m}}\ce{^{\infty}{1}} $
Σ:(u,u,0)	$\ce{^{2}{m}}\ce{^{-1}{m}}\ce{^{1}{m}}\ce{^{\infty}{1}} $
Z:(u,1/2,0)	$\ce{^{m}{m}}\ce{^{1}{m}}\ce{^{1}{m}}\ce{^{\infty}{1}} $
A:(u,v,0)	$\ce{^{m}{2/}}\ce{^{1}{m}}\ce{^{\infty}{1}} $
B:(u,1/2,w)	$\ce{^{m}{2/}}\ce{^{1}{m}}\ce{^{\infty}{1}} $
C:(u,u,w)	$\ce{^{-1}{2/}}\ce{^{2}{m}}\ce{^{\infty}{1}} $
GP:(u,v,w)	$\ce{^{m}{-1}}\ce{^{\infty}{1}} $

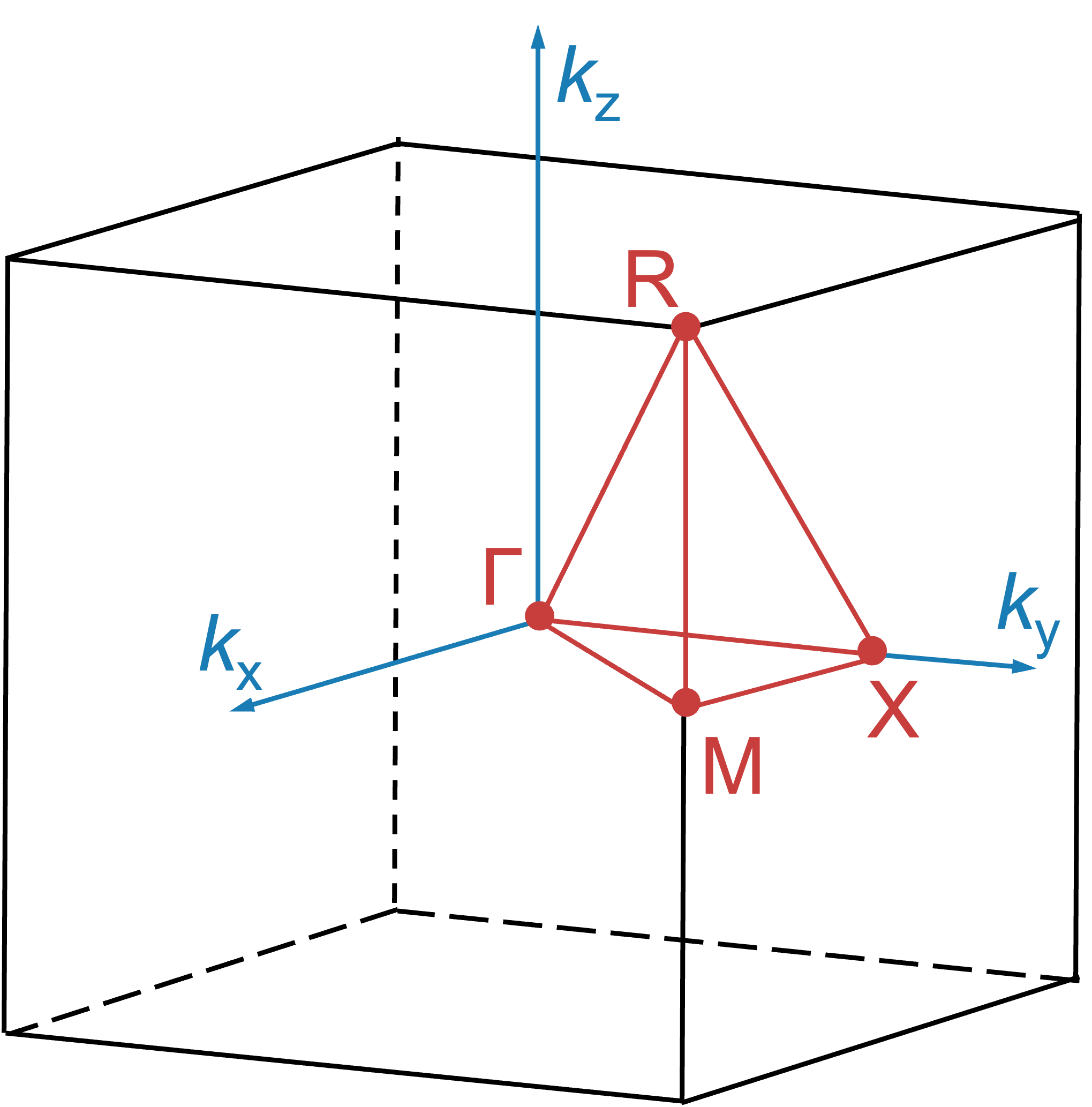
Spin Brillouin Zone

Band Representations (Magnon)

12h

k-vector	k-vector-G↑	A1↑G(12)
Γ:(0,0,0)	Γ:(0,0,0)	$Γ_{1}^{S,+}(2)⊕Γ_{2}^{S,+}Γ_{3}^{S,+}(4)⊕Γ_{4}^{S,-}(6) $
M:(1/2,1/2,0)	M:(1/2,1/2,0)	$M_{1}^{S,+}(2)⊕M_{2}^{S,+}(2)⊕M_{3}^{S,-}(2)⊕M_{4}^{S,+}(2)⊕2M_{4}^{S,-}(2) $
R:(1/2,1/2,1/2)	R:(1/2,1/2,1/2)	$R_{4}^{S,+}(6)⊕R_{4}^{S,-}(6) $
X:(0,1/2,0)	X:(0,1/2,0)	$2X_{1}^{S,+}(2)⊕X_{2}^{S,+}(2)⊕X_{2}^{S,-}(2)⊕2X_{4}^{S,-}(2) $
Δ:(0,v,0)	Δ:(0,v,0)	$4Δ_{1}^{S}(2)⊕Δ_{3}^{S}(2)⊕Δ_{4}^{S}(2) $
Λ:(u,u,u)	Λ:(u,u,u)	$2Λ_{1}^{S}(2)⊕2Λ_{2}^{S}Λ_{3}^{S}(4) $
S:(u,1/2,u)	S:(u,1/2,u)	$3S_{1}^{S}(2)⊕3S_{2}^{S}(2) $
Σ:(u,u,0)	Σ:(u,u,0)	$5Σ_{1}^{S}(2)⊕Σ_{2}^{S}(2) $
T:(1/2,1/2,w)	T:(1/2,1/2,w)	$T_{1}^{S}(2)⊕T_{2}^{S}(2)⊕2T_{3}^{S}(2)⊕2T_{4}^{S}(2) $
Z:(u,1/2,0)	Z:(u,1/2,0)	$4Z_{1}^{S}(1)⊕2 Z_{3}^{S}(1)⊕6Z_{4}^{S}(1)$	Spin Splitting
A:(u,v,0)	A:(u,v,0)	$10A_{1}^{S}(1)⊕2A_{2}^{S}(1)$	Spin Splitting
B:(u,1/2,w)	B:(u,1/2,w)	$6B_{1}^{S}(1)⊕6B_{2}^{S}(1)$	Spin Splitting
C:(u,u,w)	C:(u,u,w)	$6C_{1}^{S}(2) $
GP:(u,v,w)	GP:(u,v,w)	$12GP_{1}^{S}(1)$	Spin Splitting

24k

k-vector	k-vector-G↑	A'↑G(24)
Γ:(0,0,0)	Γ:(0,0,0)	$Γ_{1}^{S,+}(2)⊕Γ_{2}^{S,+}Γ_{3}^{S,+}(4)⊕Γ_{4}^{S,+}(6)⊕2Γ_{4}^{S,-}(6) $
M:(1/2,1/2,0)	M:(1/2,1/2,0)	$3M_{1}^{S,+}(2)⊕M_{2}^{S,+}(2)⊕2M_{2}^{S,-}(2)⊕M_{3}^{S,+}(2)⊕2M_{3}^{S,-}(2)⊕M_{4}^{S,+}(2)⊕2M_{4}^{S,-}(2) $
R:(1/2,1/2,1/2)	R:(1/2,1/2,1/2)	$R_{1}^{S,+}(2)⊕R_{2}^{S,+}R_{3}^{S,+}(4)⊕R_{4}^{S,+}(6)⊕2R_{4}^{S,-}(6) $
X:(0,1/2,0)	X:(0,1/2,0)	$3X_{1}^{S,+}(2)⊕X_{2}^{S,+}(2)⊕2X_{2}^{S,-}(2)⊕X_{3}^{S,+}(2)⊕2X_{3}^{S,-}(2)⊕X_{4}^{S,+}(2)⊕2X_{4}^{S,-}(2) $
Δ:(0,v,0)	Δ:(0,v,0)	$5Δ_{1}^{S}(2)⊕Δ_{2}^{S}(2)⊕3Δ_{3}^{S}(2)⊕3Δ_{4}^{S}(2) $
Λ:(u,u,u)	Λ:(u,u,u)	$4Λ_{1}^{S}(2)⊕4Λ_{2}^{S}Λ_{3}^{S}(4) $
S:(u,1/2,u)	S:(u,1/2,u)	$8S_{1}^{S}(2)⊕4S_{2}^{S}(2) $
Σ:(u,u,0)	Σ:(u,u,0)	$8Σ_{1}^{S}(2)⊕4Σ_{2}^{S}(2) $
T:(1/2,1/2,w)	T:(1/2,1/2,w)	$5T_{1}^{S}(2)⊕T_{2}^{S}(2)⊕3T_{3}^{S}(2)⊕3T_{4}^{S}(2) $
Z:(u,1/2,0)	Z:(u,1/2,0)	$10Z_{1}^{S}(1)⊕2Z_{2}^{S}(1)⊕6Z_{3}^{S}(1)⊕6Z_{4}^{S}(1)$	Spin Splitting
A:(u,v,0)	A:(u,v,0)	$16A_{1}^{S}(1)⊕8A_{2}^{S}(1)$	Spin Splitting
B:(u,1/2,w)	B:(u,1/2,w)	$16B_{1}^{S}(1)⊕8B_{2}^{S}(1)$	Spin Splitting
C:(u,u,w)	C:(u,u,w)	$12C_{1}^{S}(2) $
GP:(u,v,w)	GP:(u,v,w)	$24GP_{1}^{S}(1)$	Spin Splitting

24l

k-vector	k-vector-G↑	A'↑G(24)
Γ:(0,0,0)	Γ:(0,0,0)	$Γ_{1}^{S,+}(2)⊕Γ_{2}^{S,+}Γ_{3}^{S,+}(4)⊕Γ_{4}^{S,+}(6)⊕2Γ_{4}^{S,-}(6) $
M:(1/2,1/2,0)	M:(1/2,1/2,0)	$M_{1}^{S,+}(2)⊕2M_{1}^{S,-}(2)⊕3M_{2}^{S,+}(2)⊕M_{3}^{S,+}(2)⊕2M_{3}^{S,-}(2)⊕M_{4}^{S,+}(2)⊕2M_{4}^{S,-}(2) $
R:(1/2,1/2,1/2)	R:(1/2,1/2,1/2)	$R_{1}^{S,-}(2)⊕R_{2}^{S,-}R_{3}^{S,-}(4)⊕2R_{4}^{S,+}(6)⊕R_{4}^{S,-}(6) $
X:(0,1/2,0)	X:(0,1/2,0)	$2X_{1}^{S,+}(2)⊕X_{1}^{S,-}(2)⊕2X_{2}^{S,+}(2)⊕X_{2}^{S,-}(2)⊕2X_{3}^{S,+}(2)⊕X_{3}^{S,-}(2)⊕3X_{4}^{S,-}(2) $
Δ:(0,v,0)	Δ:(0,v,0)	$5Δ_{1}^{S}(2)⊕Δ_{2}^{S}(2)⊕3Δ_{3}^{S}(2)⊕3Δ_{4}^{S}(2) $
Λ:(u,u,u)	Λ:(u,u,u)	$4Λ_{1}^{S}(2)⊕4Λ_{2}^{S}Λ_{3}^{S}(4) $
S:(u,1/2,u)	S:(u,1/2,u)	$4S_{1}^{S}(2)⊕8S_{2}^{S}(2) $
Σ:(u,u,0)	Σ:(u,u,0)	$8Σ_{1}^{S}(2)⊕4Σ_{2}^{S}(2) $
T:(1/2,1/2,w)	T:(1/2,1/2,w)	$T_{1}^{S}(2)⊕5 T_{2}^{S}(2)⊕3T_{3}^{S}(2)⊕3T_{4}^{S}(2) $
Z:(u,1/2,0)	Z:(u,1/2,0)	$6Z_{1}^{S}(1)⊕6Z_{2}^{S}(1)⊕2Z_{3}^{S}(1)⊕10Z_{4}^{S}(1)$	Spin Splitting
A:(u,v,0)	A:(u,v,0)	$16A_{1}^{S}(1)⊕8A_{2}^{S}(1)$	Spin Splitting
B:(u,1/2,w)	B:(u,1/2,w)	$8B_{1}^{S}(1)⊕16B_{2}^{S}(1)$	Spin Splitting
C:(u,u,w)	C:(u,u,w)	$12C_{1}^{S}(2) $
GP:(u,v,w)	GP:(u,v,w)	$24GP_{1}^{S}(1)$	Spin Splitting

48n

k-vector	k-vector-G↑	A↑G(48)
Γ:(0,0,0)	Γ:(0,0,0)	$Γ_{1}^{S,+}(2)⊕Γ_{1}^{S,-}(2)⊕Γ_{2}^{S,+}Γ_{3}^{S,+}(4)⊕Γ_{2}^{S,-}Γ_{3}^{S,-}(4)⊕3Γ_{4}^{S,+}(6)⊕3Γ_{4}^{S,-}(6) $
M:(1/2,1/2,0)	M:(1/2,1/2,0)	$3M_{1}^{S,+}(2)⊕3M_{1}^{S,-}(2)⊕3M_{2}^{S,+}(2)⊕3M_{2}^{S,-}(2)⊕3M_{3}^{S,+}(2)⊕3M_{3}^{S,-}(2)⊕3M_{4}^{S,+}(2)⊕3M_{4}^{S,-}(2) $
R:(1/2,1/2,1/2)	R:(1/2,1/2,1/2)	$R_{1}^{S,+}(2)⊕R_{1}^{S,-}(2)⊕R_{2}^{S,+}R_{3}^{S,+}(4)⊕R_{2}^{S,-}R_{3}^{S,-}(4)⊕3R_{4}^{S,+}(6)⊕3R_{4}^{S,-}(6) $
X:(0,1/2,0)	X:(0,1/2,0)	$3X_{1}^{S,+}(2)⊕3X_{1}^{S,-}(2)⊕3X_{2}^{S,+}(2)⊕3X_{2}^{S,-}(2)⊕3X_{3}^{S,+}(2)⊕3X_{3}^{S,-}(2)⊕3X_{4}^{S,+}(2)⊕3X_{4}^{S,-}(2) $
Δ:(0,v,0)	Δ:(0,v,0)	$6Δ_{1}^{S}(2)⊕6Δ_{2}^{S}(2)⊕6Δ_{3}^{S}(2)⊕6Δ_{4}^{S}(2) $
Λ:(u,u,u)	Λ:(u,u,u)	$8Λ_{1}^{S}(2)⊕8Λ_{2}^{S}Λ_{3}^{S}(4) $
S:(u,1/2,u)	S:(u,1/2,u)	$12S_{1}^{S}(2)⊕12S_{2}^{S}(2) $
Σ:(u,u,0)	Σ:(u,u,0)	$12Σ_{1}^{S}(2)⊕12Σ_{2}^{S}(2) $
T:(1/2,1/2,w)	T:(1/2,1/2,w)	$6T_{1}^{S}(2)⊕6T_{2}^{S}(2)⊕6T_{3}^{S}(2)⊕6T_{4}^{S}(2) $
Z:(u,1/2,0)	Z:(u,1/2,0)	$12Z_{1}^{S}(1)⊕12Z_{2}^{S}(1)⊕12Z_{3}^{S}(1)⊕12Z_{4}^{S}(1)$	Spin Splitting
A:(u,v,0)	A:(u,v,0)	$24A_{1}^{S}(1)⊕24A_{2}^{S}(1)$	Spin Splitting
B:(u,1/2,w)	B:(u,1/2,w)	$24B_{1}^{S}(1)⊕24B_{2}^{S}(1)$	Spin Splitting
C:(u,u,w)	C:(u,u,w)	$24C_{1}^{S}(2) $
GP:(u,v,w)	GP:(u,v,w)	$48GP_{1}^{S}(1)$	Spin Splitting